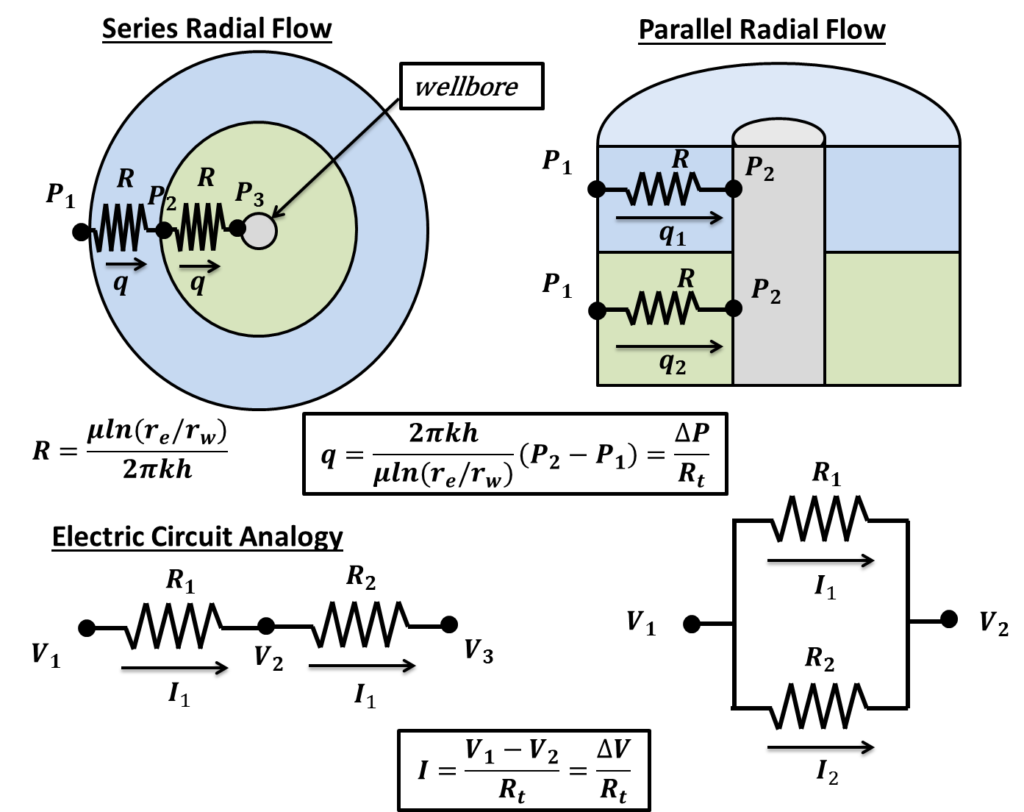
Average Permeability of Flow Units in Parallel and in Series (Radial Flow)

Everything we just applied to linear flow, extends to radial flow. Nothing too different! The same analogy works! The only difference is we apply Darcy’s law for radial flow. We will know work through the derivations of average permeability for series radial flow and parallel radial flow.

Series Radial Flow-Harmonic Average

Consider radial flow for flow units in series as shown in the diagram below:

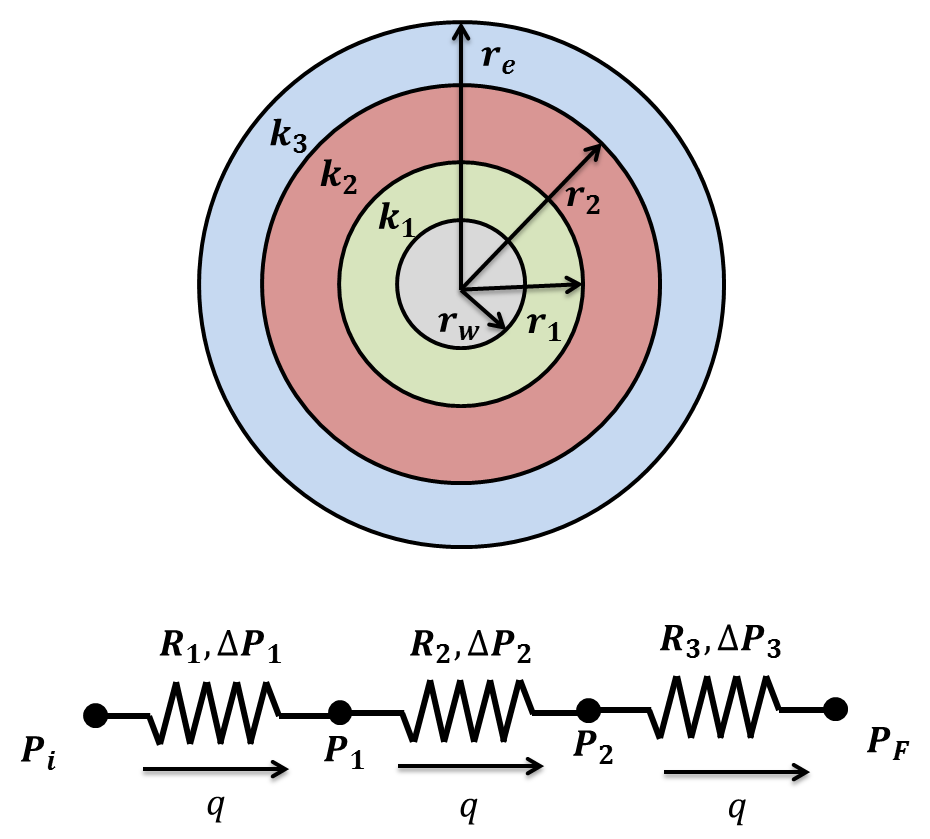
Recall, that flow going through flow units in series can be treated as resistors in series. Using the same rules we applied in the previous post, we can derive the following expression:

(1) $\begin{equation*}\ \triangle P_t =\sum_{i=1}^{3}\triangle P_i= \triangle P_1 + \triangle P_2 + \triangle P_3 \end{equation*}$

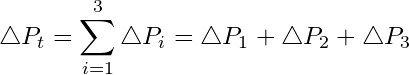
Using Darcy’s law for radial flow, the total pressure drop ( $\triangle P_t = P_i-P_F$ ) across the entire system is given by the following expression:

(2) $\begin{equation*} \triangle P = \frac{qu}{2\pi h}\frac{\ln({\frac{r_e}{r_w}})}{k_{avg}} \end{equation*}$

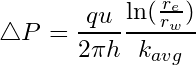
Using Darcy’s law, the total pressure drop across a flow unit ( $\triangle P_i$ ) is given by the following expression:

(3) $\begin{equation*} \triangle P = \frac{qu}{2\pi h}\frac{\ln({\frac{r_i}{r_{i-1}}})}{k_i} \end{equation*}$

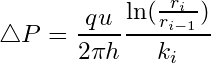
Substituting Equations (2) and (3) into Equation (1) we can develop the following expression:

(4) $\begin{equation*} \frac{qu}{2\pi h}\frac{\ln({\frac{r_e}{r_w}})}{k_{avg}} =\frac{qu}{2\pi h}\frac{\ln({\frac{r_1}{r_{w}}})}{k_1} +\frac{qu}{2\pi h}\frac{\ln({\frac{r_2}{r_{1}}})}{k_2} +\frac{qu}{2\pi h}\frac{\ln({\frac{r_3}{r_{2}}})}{k_3} \end{equation*}$

Assuming the height of each flow unit is identical, Equation (4) can be reduced to the following in terms of the average permeability:

(5) $\begin{equation*} k_{avg} =\frac{\ln({\frac{r_e}{r_w}})}{\frac{\ln({\frac{r_1}{r_{w}}})}{k_1} + \frac{\ln({\frac{r_2}{r_{1}}})}{k_2} + \frac{\ln({\frac{r_3}{r_{2}}})}{k_3}} \end{equation*}$

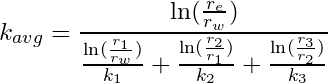
A more general equation that describes the average permeability of $n$ flow units arranged in series is the following:

$\boxed{k_{avg} = \frac{\ln({\frac{r_e}{r_{w}})}}{\sum_{i=1}^{n}\frac{\ln({\frac{r_i}{r_{i-1}}})}{k_i}}}$

Parallel Radial Flow-Weighted Average

Consider radial flow for flow units in parallel as shown in the diagram below:

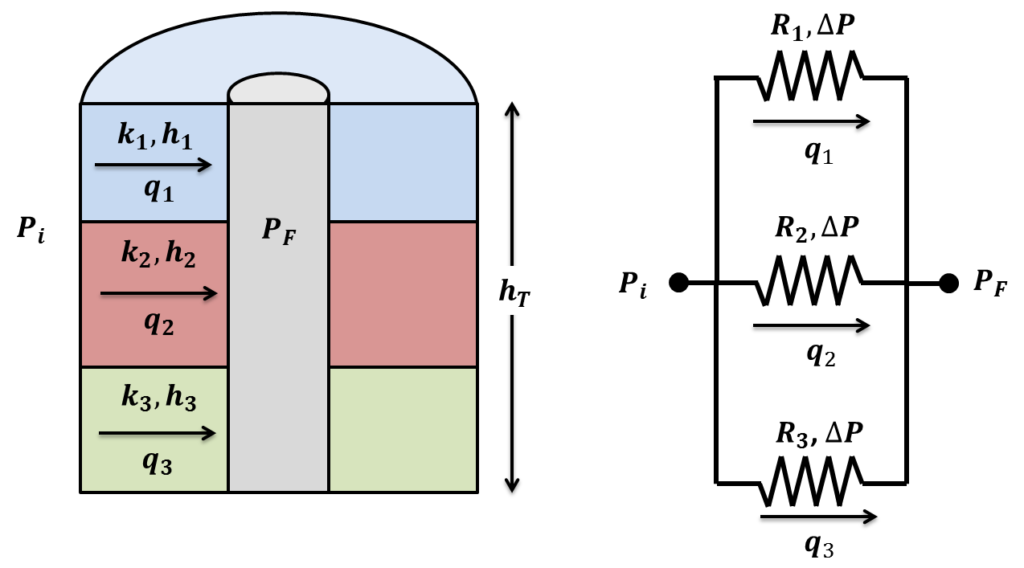
Recall, that flow going through flow units in parallel can be treated as resistors in parallel. Using the same rules we applied in the previous post, we can derive the following expression:

(6) $\begin{equation*}\ q_t =\sum_{i=1}^{3}q_i= q_1 + q_2 + q_3 \end{equation*}$

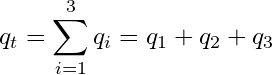
Using Darcy’s law, the total flow rate (q_t) across the entire system is given by the following expression:

(7) $\begin{equation*} q_t =\frac{2\pi \triangle P}{u\ln({\frac{r_e}{r_w}})}k_{avg}h_T \end{equation*}$

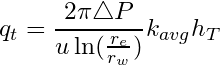
Using Darcy’s law, the total flow rate across a flow unit ( $q_i$ ) is given by the following expression:

(8) $\begin{equation*} q_i =\frac{2\pi \triangle P}{u\ln({\frac{r_e}{r_w}})}k_i h_i \end{equation*}$

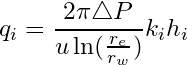
Substituting Equations (7) and (8) into Equation (6) we can develop the following expression:

(9) $\begin{equation*} \frac{2\pi \triangle P}{u\ln({\frac{r_e}{r_w}})}k_{avg}h_T = \frac{2\pi \triangle P}{u\ln({\frac{r_e}{r_w}})}k_1 h_1 + \frac{2\pi \triangle P}{u\ln({\frac{r_e}{r_w}})}k_2 h_2 + \frac{2\pi \triangle P}{u\ln({\frac{r_e}{r_w}})}k_3 h_3 \end{equation*}$

Assuming the radius of each flow unit is identical, Equation (9) can be reduced to the following in terms of the average permeability:

(10) $\begin{equation*} k_{avg} =\frac{k_{1}h_{1} + k_{2}h_{2} + k_{3}h_{3}}{h_T} \end{equation*}$

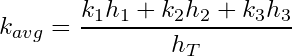
A more general equation that describes the average permeability of $n$ flow units arranged in parallel is the following:

$\boxed{k_{avg} = \frac{\sum_{i=1}^{n}k_{i}h_{i}}{h_T}}$

**Note: This is the exact same expression for series parallel flow! That makes it easy to remember.