Back to: General Petroleum Engineering
A dry gas reservoir is a reservoir that contains only gas. Further, the produced fluid is only gas, i.e. no liquid condensate drops out at the surface. Once again, to produce the material balance equation for a dry gas reservoir, we must consider the initial state and current state of the reservoir. At the same time, must also be able to picture the phase diagram for a dry gas reservoir. Consider the states of a wet gas reservoir as illustrated below:
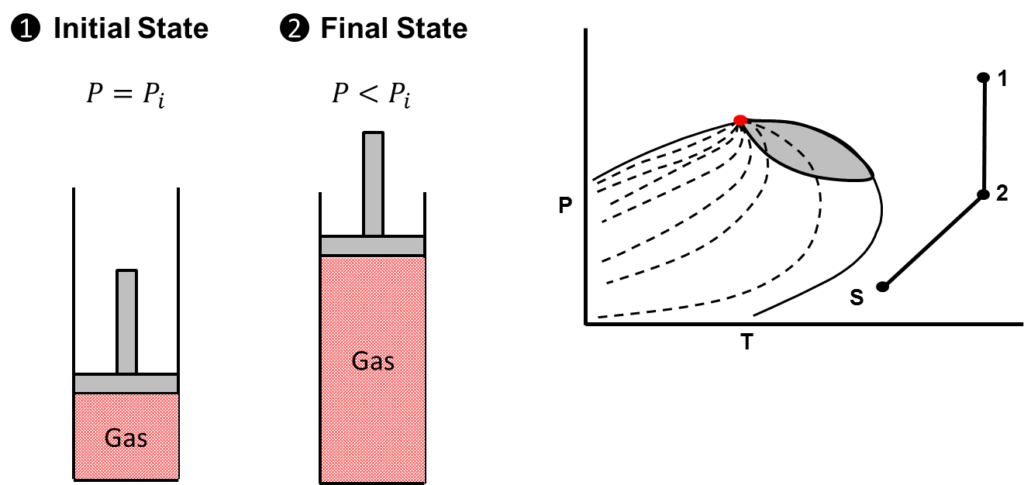
From the figure above, it should be clear that at the initial reservoir pressure and final pressure, a dry gas reservoir only contains gas. As the fluid rises to surface, only gas is produced at the separator. The phase diagram of a dry gas reservoir shows the initial state indicated by the number 1 and the final state indicated by the number 2. Separator conditions are indicated by the letter “S”. Again, consider the macrocopic material balance equation. Because we know the reservoir states and general pressure decline path of a dry gas reservoir on a phase diagram, we can intelligently begin to eliminate terms that do not apply. The results are shown below:
(G_{fg})_i(\overbrace{\xcancel{B_{tg}}}^{B_i}-\overbrace{\xcancel{B_{tg_i}}}^{B_{g_i}})+\xcancel{N_i}({B_{to}}-B_{to_i}) + W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= (G_p-\xcancel{G_I})(\frac{B_g-\xcancel{B_oR_v}}{1-\xcancel{R_vR_s}}) + N_p(\frac{\xcancel{B_o}-B_g\xcancel{R_s}}{1-\xcancel{R_sR_v}})+\xcancel{(W_p-W_I)B_w}-
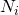 = 0: no oil is initially in place
= 0: no oil is initially in place 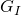 = 0: assume no gas injected into the reservoir
= 0: assume no gas injected into the reservoir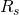 =undefined: no solution gas evolving out of the oil
=undefined: no solution gas evolving out of the oil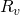 = undefined: no condensate dropping out of the gas
= undefined: no condensate dropping out of the gas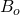 = undefined: no oil expanding to surface
= undefined: no oil expanding to surface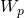 = 0 : assume negligible water production
= 0 : assume negligible water production
After eliminating the unnecessary terms, the material balance equation for a gas condensate reservoir becomes the following:
(1)\;\;\;\;\; (G_{fg})_i(B_i-B_{g_i})+W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= G_pB_gThe above result should makes sense. We initially have gas in the reservoir, thus ![]() is defined. No matter how far the pressure declines, we always have single phase gas in the reservoir. Therefore, two phase gas formation volume factor
is defined. No matter how far the pressure declines, we always have single phase gas in the reservoir. Therefore, two phase gas formation volume factor ![]() gets converted to the single phase gas formation volume factor
gets converted to the single phase gas formation volume factor ![]() . On the phase diagram, as the fluid arrives to the surface, only a single fluid is produced, i.e. gas. Therefore
. On the phase diagram, as the fluid arrives to the surface, only a single fluid is produced, i.e. gas. Therefore ![]() is undefined because liquid never drops out of the gas.
is undefined because liquid never drops out of the gas. ![]() and
and ![]() is undefined because oil never expands to the surface. The equation below shows which terms are eliminated if one assumes a volumetric reservoir:
is undefined because oil never expands to the surface. The equation below shows which terms are eliminated if one assumes a volumetric reservoir:
- Assume volumetric reservoir:
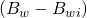 =0 ,
=0 , 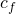 = 0, and
= 0, and 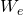 =0
=0
After eliminating terms with the volumetric assumption, the material balance equation for a volumetric gas condensate reservoir is the following:
(2)\;\;\;\;\;(G_{fg})_i(B_i-B_{g_i})= G_pB_gThere we have it! The macrocopic material balance equation combined with our knowledge of phase behavior results in a simple expression to describe the production of a dry gas reservoir. In summary, we have applied the single macroscopic material balance equation to describe several different reservoir types.