Back to: General Petroleum Engineering
When dealing with rocks, we are always interested in the fracture pressure. One application of fracture pressure is in drilling and completions. If we fracture the formation while we are drillng due to excessive mud weight, lost circulation could occur in the well bore which could eventually lead to a blow out if we are not careful. To estimate fracture pressure, we usually need to determine the effective stress or vertical grain-to-grain matrix stress on the rock. The effective stress is essentially the vertical compression load the rock feels. Using the concepts we discussed previously we are going to show how the effective stress can be determined. The figure below shows a cartoon illustration of the vertical stresses encountered in the formation:
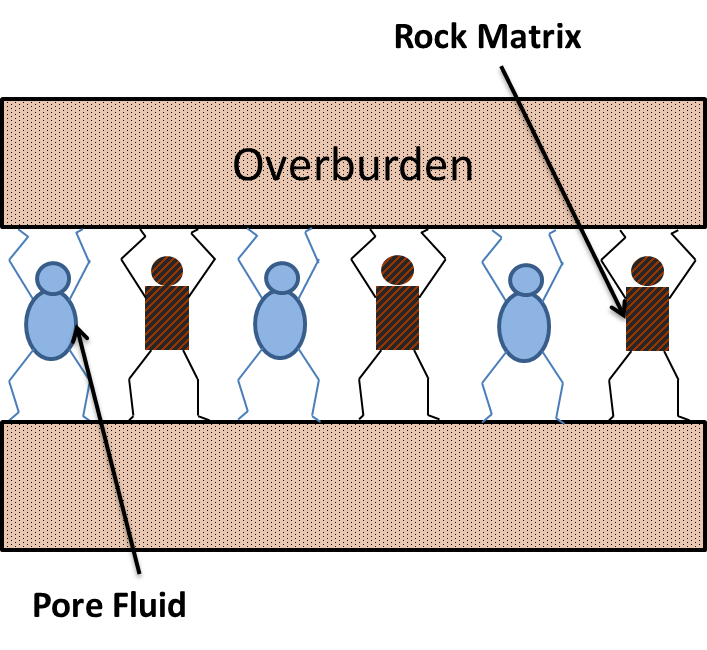
The weight of the overburden is supported by (1) the vertical grain-to-grain matrix stress and (2) the pore fluid pressure. Because the rock is static, the forces must be in static equilibrium with each other. The system of rock grains can be packed in different configurations so it can be difficult to visualize a force balance on this type of system. We simplify this system by replacing it with a spring-piston model as shown in the figure below:
The spring represents the resistance of the rock grains (i.e. the effective stress). The pore pressure at the piston interface is represented by a column of water that runs all the way to the surface unrestricted. Note: Because we assume the flow path to surface is unrestricted, it is considered normally pressured and we can use the relation 
. Using this spring-piston analogy we can easily determine the effective stress on the rock. The figure below shows a free body diagram of the top piston:
Because the piston is static, the overburden stress must be equivalent to the sum of the pore pressure and effective stress. We can then derive an expression to calculate the effective stress. The expression we end up with is the following:
(1) 
where:
= the overburden stress, psi
= the effective stress, psi
= pore pressure, psi
The effective stress on the rock turns out to be equal to the difference between the overburden stress and the pore pressure.
In summary, we were able to determine the compression load felt by the rock matrix using a spring-piston analogy and simple statics. Knowing this we can now move forward to estimating the horizontal stress imposed on the rock matrix using solid mechanics relationships. After that we can determine a fracture pressure.