Previously, we learned that the rock in the formation is subject to a vertical compression load called the effective stress. In general if you apply a vertical compression load to any solid element, it will expand horizontally. Take cookie dough for instance. If you smush it vertically between both hands, the cookie dough will flatten out and expand outwards like a pancake. Well, the exact same thing happens to a rock. The only difference is it requires a lot more force to do it. The figure below shows the effect of vertical and horizontal stresses on a rock under different loading conditions:

The image in the middle of the figure shows how the rock would deform if we placed a compression load on it at the surface. It would flatten outward like the cookie analogy mentioned earlier. The image on the far right shows the stress loads acting on the rock in the formation. In the formation, we assume the rock is NOT allowed to expand because the surrounding rock applies a horizontal stress. This loading situation is often denoted as uniaxial strain compaction because the rock only deforms or changes length in the vertical direction. The relationship between the vertical effective stress and horizontal matrix stress can be determined from the fundamentals of solid mechanics. Consider a three dimensional rock element in the formation as shown in the figure below:

A rock element in the formation is subject to multi-axial loading in three directions. For simplicity, we will also assume the rock element is isotropic. The equations that describe this type of loading are given by the following expressions derived from Hooke’s law for a homogeneous isotropic material :
(1) 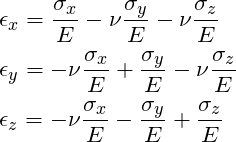
where ![]() is the stress in the z-direction, i.e. the effective stress (
is the stress in the z-direction, i.e. the effective stress (![]() ),
), ![]() is the stress in the x-direction,
is the stress in the x-direction, ![]() is the stress in the y-direction,
is the stress in the y-direction, ![]() is Young’s modulus of the rock, and
is Young’s modulus of the rock, and ![]() is possion’s ratio of the rock. Because of the uniaxial strain condition we know that the rock cannot deform in the horizontal direction. Therefore
is possion’s ratio of the rock. Because of the uniaxial strain condition we know that the rock cannot deform in the horizontal direction. Therefore ![]() . We also know that
. We also know that ![]() (Recall, we know how to calculate this!!). Knowing the value of these three variables, we can solve for the remaining unknowns in the Hooke’s law equations (1). We will now proceed in deriving the relationship between the horizontal matrix stress and the vertical effective stress:
(Recall, we know how to calculate this!!). Knowing the value of these three variables, we can solve for the remaining unknowns in the Hooke’s law equations (1). We will now proceed in deriving the relationship between the horizontal matrix stress and the vertical effective stress:
STEP 1: Substitute ![]() into the Hooke’s law expressions:
into the Hooke’s law expressions:
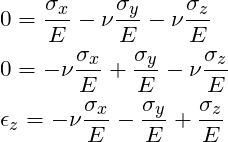
STEP2: Using the top two equations solve for ![]() and
and ![]() :
:
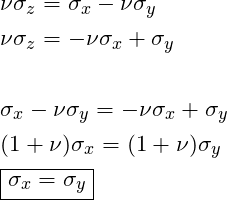
STEP3: Substitute the result into the first equation from Step 2:
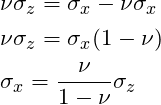
Step4: Substitute ![]() and
and ![]() :
:
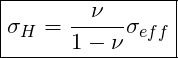
Using Solid mechanics, we were able to derive an expression relating the vertical effective stress to the horizontal matrix stress. We can use this result to help us calculate a fracture pressure! But before we jump onto the next topic, the table below shows poission ratio values for common minerals:
Table 1: Mineral Poisson’s ratios
| Mineral | Poisson’s Ratio |
| quartz | 0.09 |
| calcite | 0.32 |
| anhydrite | 0.27 |
| salt | 0.264 |
If we substitute any of the values shown in the table into our derived result, the ratio (![]() ) will be less than 1. This means that the calculated horizontal stress will be less than the overburden at any depth.
) will be less than 1. This means that the calculated horizontal stress will be less than the overburden at any depth.