A gas condensate reservoir is a reservoir that drops out liquid condensate in the reservoir as the reservoir falls below the dew point pressure. Once again, to produce the material balance equation for a gas condensate reservoir, we must consider the initial state and current state of the reservoir. In the back of our mind we must also be able to picture the phase diagram for a gas condensate reservoir. Consider the states of a gas condensate reservoir as illustrated below:
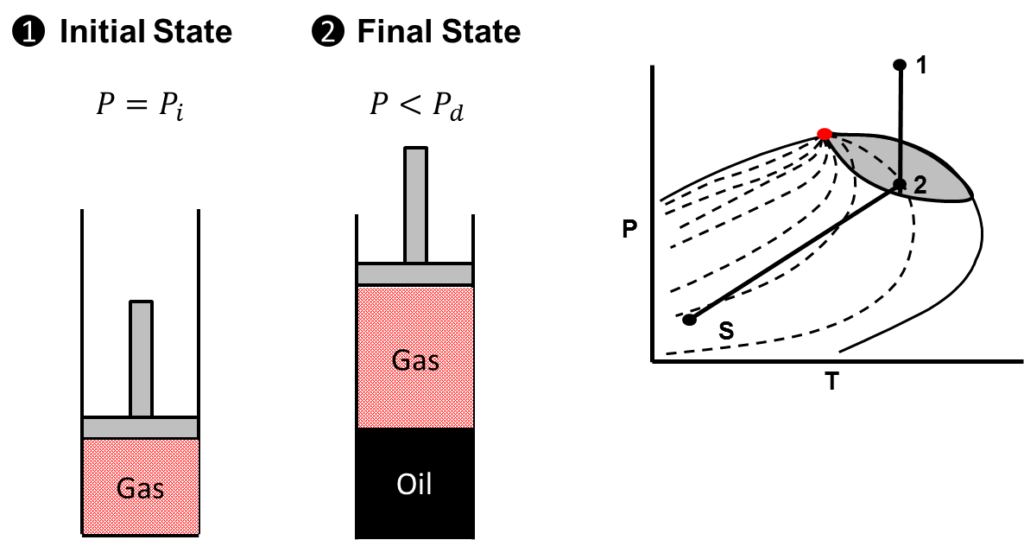
From the figure above, it should be clear that at the initial reservoir pressure, a gas condensate reservoir contains only free gas. As the pressure falls below the dew point line, condensate (liquid oil) drops out into the reservoir. A phase diagram of a gas condensate reservoir is also shown with the initial state indicated by the number 1 and the final state indicated by the number 2. Separator conditions are indicated by the letter “S”. Again, consider the macrocopic material balance equation. Because we know the reservoir states and general pressure decline path of a gas condensate reservoir on a phase diagram, we can intelligently begin to eliminate terms that do not apply. The results are shown below:
(G_{fg})_i(B_{tg}-B_{tg_i})+\xcancel{N_i}({B_{to}}-B_{to_i}) + W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= (G_p-\xcancel{G_I})(\frac{B_g-B_oR_v}{1-R_vR_s}) + N_p(\frac{B_o-B_gR_s}{1-R_sR_v})+\xcancel{(W_p-W_I)B_w}-
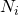 = 0: no oil is initially in place
= 0: no oil is initially in place 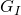 = 0: assume no gas injected into the reservoir
= 0: assume no gas injected into the reservoir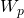 = 0 : assume negligible water production
= 0 : assume negligible water production
After eliminating the unnecessary terms, the material balance equation for a gas condensate reservoir becomes the following:
(1)\;\;\;\;\; (G_{fg})_i(B_{tg}-B_{tg_i})+W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= G_p(\frac{B_g-B_oR_v}{1-R_vR_s}) + N_p(\frac{B_o-B_gR_s}{1-R_sR_v}) The above result should makes sense. We initially have gas in the reservoir, thus ![]() is defined. When the pressure falls below the dew point line, we have two phases in the reservoir. Therefore the two phase gas formation volume factor
is defined. When the pressure falls below the dew point line, we have two phases in the reservoir. Therefore the two phase gas formation volume factor ![]() is defined. On the phase diagram, the reservoir pressure decline path enters the condensate region (highlighted in grey). Therefore
is defined. On the phase diagram, the reservoir pressure decline path enters the condensate region (highlighted in grey). Therefore ![]() is defined. When the reservoir pressure falls below the dew point, we have two fluids from the reservoir that are produced at the surface. Therefore
is defined. When the reservoir pressure falls below the dew point, we have two fluids from the reservoir that are produced at the surface. Therefore ![]() ,
, ![]() , and
, and ![]() are defined. The reason
are defined. The reason ![]() is defined is because some of the oil revaporizes into gas as the fluid exits the condensate region. The equation below shows which terms are eliminated if one assumes a volumetric reservoir:
is defined is because some of the oil revaporizes into gas as the fluid exits the condensate region. The equation below shows which terms are eliminated if one assumes a volumetric reservoir:
- Assume volumetric reservoir:
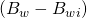 =0 ,
=0 , 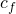 = 0, and
= 0, and 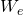 =0
=0
After eliminating terms with the volumetric assumption, the material balance equation for a volumetric gas condensate reservoir is the following:
(2)\;\;\;\;\; (G_{fg})_i(B_{tg}-B_{tg_i}) = G_p(\frac{B_g-B_oR_v}{1-R_vR_s}) + N_p(\frac{B_o-B_gR_s}{1-R_sR_v})We keep chugging along guys and dominating at the same time. A gas condensate reservoir is one of the most difficult reservoirs to characterize. However with the macroscopic material balance equation, one was able to do it. In the next post, we will look at deriving the material balance equation for a wet gas reservoir.