A saturated reservoir is a reservoir where the reservoir pressure has fallen below the bubble point pressure line. Black oil and volatile oil reservoirs exhibit saturated reservoir behavior, thus their material balance derivations are identical. Once again, to evaluate any material balance situation, we must consider the initial state and current state of the reservoir. We must also keep in mind the phase behavior of the fluid we are observing. Consider the states of an saturated reservoir as illustrated below:
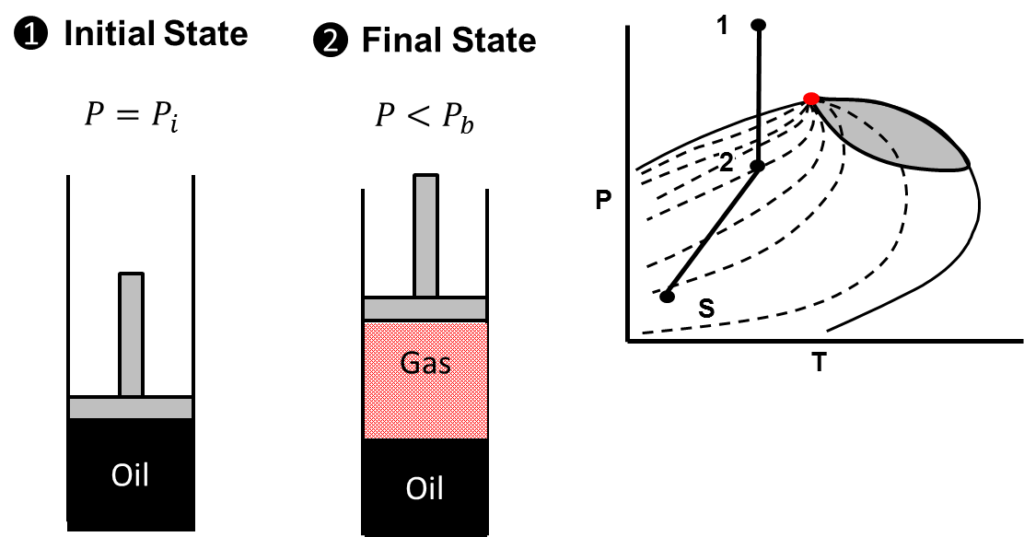
From the figure above it should be clear that at the initial reservoir pressure, a saturated reservoir contains oil and no free gas. As the reservoir pressure falls below the bubble point line, free gas begins to evolve in the reservoir. A phase diagram of a saturated reservoir is also shown with the initial state indicated by the number 1 and the final state indicated by the number 2. Separator conditions are indicated by the letter “S”. Again, consider the macroscopic material balance equation. Because we know the reservoir states and the general pressure decline path of a saturated reservoir on a phase diagram, we can intelligently begin to eliminate terms that do not apply. The results are shown below:
\xcancel{(G_{fg})_i}(B_{tg}-B_{tg_i})+N_i({B_{to}}-B_{to_i}) + W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= (G_p-\xcancel{G_I})(\frac{B_g-\xcancel{B_oR_v}}{1-\xcancel{R_vR_s}}) + N_p(\frac{B_o-B_gR_s}{1-\xcancel{R_sR_v}})+\xcancel{(W_p-W_I)B_w}-
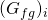 =0: No gas is initially in place
=0: No gas is initially in place 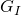 = 0: assume no gas injected into the reservoir
= 0: assume no gas injected into the reservoir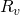 = 0 : No condensate dropping out of gas because we are to the left side of the critical point
= 0 : No condensate dropping out of gas because we are to the left side of the critical point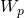 = 0 : assume negligible water production
= 0 : assume negligible water production
After eliminating the unnecessary terms, the material balance equation for a saturated reservoir becomes the following:
(1)\;\;\;\;\; N_i({B_{to}}-B_{to_i}) + W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= (G_p)B_g + N_p(B_o-B_gR_s)This result should make sense. When the pressure falls below the bubble point pressure, we have a gas phase in the reservoir. This means ![]() is defined. Further, we have multiple phases in the reservoir, therefore the two phase oil formation volume factor (
is defined. Further, we have multiple phases in the reservoir, therefore the two phase oil formation volume factor (![]() ) is defined. The above result can be simplified further if we assume a volumetric reservoir. Recall, for a volumetric reservoir one neglects water and rock compressibilities and assumes no aquifer support. The equation below shows which terms are eliminated if one assumes a volumetric reservoir:
) is defined. The above result can be simplified further if we assume a volumetric reservoir. Recall, for a volumetric reservoir one neglects water and rock compressibilities and assumes no aquifer support. The equation below shows which terms are eliminated if one assumes a volumetric reservoir:
- Assume volumetric reservoir:
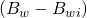 =0 ,
=0 , 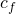 = 0, and
= 0, and 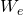 =0
=0
After eliminating terms with the volumetric assumption, the material balance equation for a volumetric saturated reservoir is the following:
(2)\;\;\;\;\;N_i({B_{to}}-B_{to_i})= (G_p)B_g + N_p(B_o-B_gR_s)How was that? The material balance derivation for a saturated reservoir is just as easy as the material balance derivation for an undersaturated reservoir. In summary, if one considers the states of the reservoir and the phase diagram, the material balance derivations are intuitive. I have not found an easier way. We will continue to apply this approach going forward.