If one understands thermodynamic states, one can get really good at deriving material balance relationships for different reservoirs. It’s simple, your first state is initial reservoir pressure and your second state is a pressure below reservoir pressure. For every material balance situation you are evaluating the reservoir at states during the depletion process. Then you can evaluate the data to determine what drive indices are present. Consider the states of an undersaturated reservoir as illustrated below:
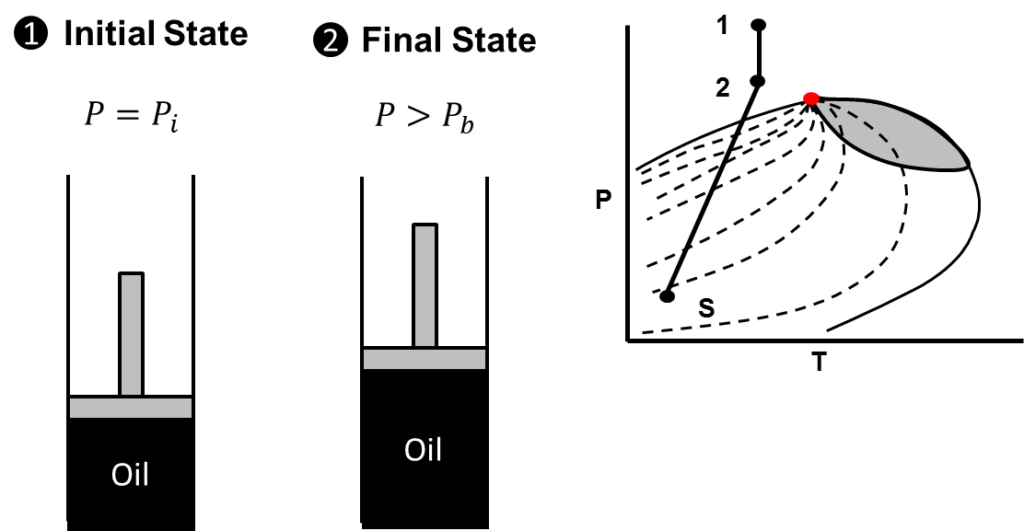
From the figure above, it is clear that the initial state is evaluated at the initial reservoir pressure and the second state is evaluated at a pressure above the bubble point. A phase diagram for an undersaturated reservoir with the states is also shown. Further the separator conditions are indicated by the letter “S”. Consider the long material balance equation. Because we know the reservoir states and the general pressure decline path of an undersaturated reservoir on a phase diagram, we can intelligently begin to eliminate terms that do not apply. The results are shown below:
Step 1: Eliminate unnecessary terms by considering the reservoir states and the phase diagram:
\xcancel{(G_{fg})_i}(B_{tg}-B_{tg_i})+N_i(\overbrace{\xcancel{B_{to}}}^{B_o}-\overbrace{\xcancel{B_{to_i})}}^{B_{oi}} + W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e \\= (G_p-G_I)(\frac{\xcancel{B_g}-\xcancel{B_oR_v}}{1-\xcancel{R_vR_s}}) + N_p(\frac{B_o-\xcancel{B_gR_s}}{1-\xcancel{R_sR_v}})+\xcancel{(W_p-W_I)B_w}-
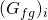 =0: No gas is initially in place
=0: No gas is initially in place 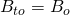 : the reservoir pressure stays above the bubble point pressure
: the reservoir pressure stays above the bubble point pressure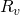 = 0 : No condensate dropping out of gas because we are to the left side of the critical point
= 0 : No condensate dropping out of gas because we are to the left side of the critical point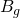 = 0 : undefined because there is never any gas in the reservoir
= 0 : undefined because there is never any gas in the reservoir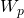 = 0 : assume negligible water production
= 0 : assume negligible water production
After reducing the unnecessary terms, the material balance equation for an under saturated reservoir becomes the following:
(1)\,\;\;\;\; N_i(B_{o}-B_{o_i}) + W_i(B_w-B_{w_i}) +v_fc_f(P_i-P) + W_e = N_pB_oIn some cases we can simplify the equation further by assuming the reservoir is volumetric. A volumetric reservoir is a reservoir where (1) water and rock compressibilities are neglected and (2) we assume there is no aquifer support (![]() ). A volumetric reservoir assumes that oil or gas is the only fluid that can expand. The equation below shows which terms are eliminated from the material balance equation when we assume a volumetric reservoir:
). A volumetric reservoir assumes that oil or gas is the only fluid that can expand. The equation below shows which terms are eliminated from the material balance equation when we assume a volumetric reservoir:
- Assume volumetric reservoir:
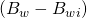 =0 ,
=0 , 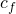 = 0, and
= 0, and 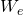 =0
=0
After eliminating terms with the volumetric assumption, the material balance equation for a volumetric undersaturated reservoir is the following:
(2)\,\;\;\;\; N_i(B_{o}-B_{o_i}) = N_pB_oHow simple was that? I hope it was simple. If you use this basic approach by considering the states and the phase diagram of a particular reservoir, one should be able to derive the material balance for any reservoir discussed so far. We will apply this same approach going forward.