Series Linear Flow-Harmonic Average
Consider linear flow for flow units in series as shown in the diagram below:

Flow going through flow units in series can be treated as resistors in series, where flow rate (![]() ) represents current (
) represents current (![]() ), pressure (
), pressure (![]() ) represents voltage (
) represents voltage (![]() ), and flow resistance (
), and flow resistance (![]() ) represents resistance (
) represents resistance (![]() ). For resistors in series, the following rules apply:
). For resistors in series, the following rules apply:
- The current is the same across each resistor.
- The sum of the potential differences across individual resistors is equal to the total voltage drop across all resistors.
This analogy can be extended to fluid flow, i.e.:
- flow rate is the same across each flow unit for flow units in series.
- the sum of the pressure drops across individual flow units is equal to the total pressure drop across all flow units
Knowing these rules, we will proceed to the derivation of average permeability for this system. Using Rule 2 the following expression can be derived:
(1) 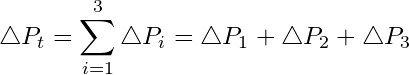
Using Darcy’s law, the total pressure drop (![]() ) across the entire system is given by the following expression:
) across the entire system is given by the following expression:
(2) 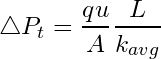
Using Darcy’s law, the total pressure drop across a flow unit (![]() ) is given by the following expression:
) is given by the following expression:
(3) 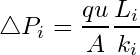
Substituting Equations (2) and (3) into Equation (1) we can develop the following expression:
(4) 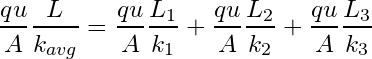
Using Rule 1 and realizing the cross sectional area of each flow unit is identical, Equation (4) can be reduced to the following in terms of the average permeability:
(5) 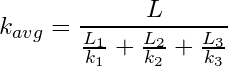
A more general equation that describes the average permeability of ![]() flow units arranged in series is the following:
flow units arranged in series is the following:
![Rendered by QuickLaTeX.com \[\boxed{k_{avg} = \frac{\sum_{i=1}^{n}L_i}{\sum_{i=1}^{n}\frac{L_i}{k_i}}}\]](https://topdogengineer.com/wp-content/ql-cache/quicklatex.com-656876194b7fcbf10135e336fe6662f4_l3.png)
Parallel Linear Flow-Weighted Average
Consider linear flow for flow units in parallel as shown in the diagram below:
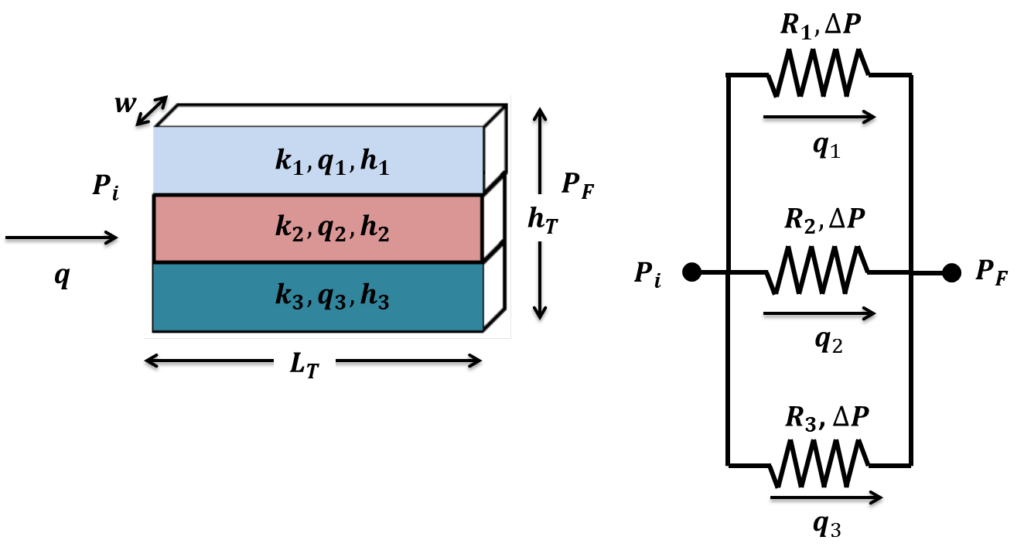
Again we apply the same analogy. For resistors in parallel, the following rules apply:
- The voltage drop is the same across each resistor.
- The sum of the current across individual resistors is equal to the total current across all resistors.
This analogy can be extended to fluid flow, i.e.:
- pressure drop is the same across each flow unit for flow units in parallel.
- the sum of the flow rates across individual flow units is equal to the total flow rate across all flow units when they are in parallel.
Knowing these rules, we will proceed to the derivation of average permeability for this system. Using Rule 1 the following expression can be derived:
(6) 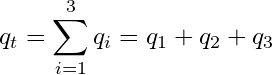
Using Darcy’s law, the total flow rate (q_t) across the entire system is given by the following expression:
(7) 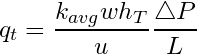
Using Darcy’s law, the total flow rate across a flow unit (![]() ) is given by the following expression:
) is given by the following expression:
(8) 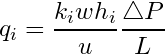
Substituting Equations (7) and (8) into Equation (6) we can develop the following expression:
(9) 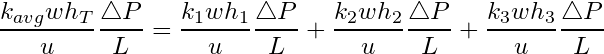
Using Rule 1 and assuming the width of each flow unit is identical, Equation (9) can be reduced to the following in terms of the average permeability:
(10) 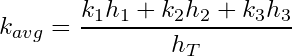
A more general equation that describes the average permeability of ![]() flow units arranged in parallel is the following:
flow units arranged in parallel is the following:
![Rendered by QuickLaTeX.com \[\boxed{k_{avg} = \frac{\sum_{i=1}^{n}k_{i}h_{i}}{h_T}}\]](https://topdogengineer.com/wp-content/ql-cache/quicklatex.com-887b1371c19cd1571e582e09310fa5e4_l3.png)